flyman Админ. спросил 5 лет назад
Как глубоко черные ящики могут уходить под воду и какое давление они могут выдержать, находясь под водой, прежде чем их раздавят?
Я непрофессионал с точки зрения авиации, так что если это не слишком много, чтобы спросить, можете ли вы ответить так легко понять, как вы можете?
flyman Админ. ответил 5 лет назад
Как глубоко черные ящики могут уходить под воду?
Они должны выдерживать глубину 20 000 футов (3,8 мили, 6,1 км) в течение 30 дней.
и сколько давления они могут выдержать?
На глубине 20 000 футов давление составляет 8900 фунтов на квадратный дюйм (psi), что в 606 раз превышает атмосферное давление на уровне моря (почти 4½ тонны на каждом квадратном дюйме поверхности)
Регистратор данных полета от AF447, около 13 000 футов глубиной в течение почти 2 лет. Все еще читаемый
Ссылки на литературу
DFDR должно быть watertight к глубине 20.000 футов в морской воде, и выдерживает на этой глубине на 30 дней
Блоки также должны выдержать статическое задавливая усилие на всем из своих 6 пунктов оси прикладной силы нагрузки 5.000 lbs на 5 минут на каждой оси.
См.: что происходит с транспондером, FDR и CVR в случае взрыва?
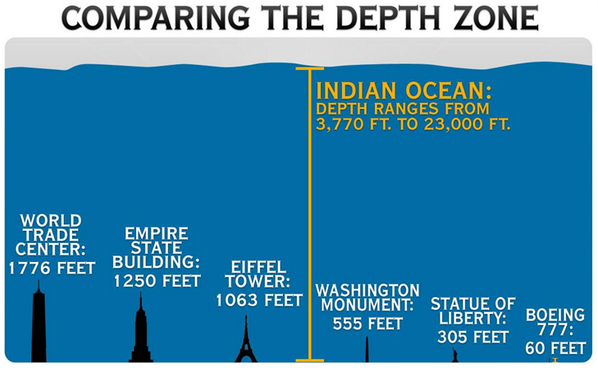
Южный коридор Индийского океана, где, по мнению официальных лиц, самолет упал, имеет глубину от 3 770 до 23 000 футов. На самой большой глубине это почти равно высоте горы Эверест (высота которой составляет 29 029 футов).
См.: глубина Индийского океана доказывает большую проблему для поисковых команд MH370
На каждые 33 фута (10,06 метра) вы идете вниз, давление увеличивается на 14,5 фунтов на квадратный дюйм (1 бар).
Смотреть также
flyman«8900 фунтов на квадратный дюйм» или примерно 626 кг/см2 (что не смешивает метрические и имперские единицы), если мое преобразование является точным. Подобно тому, как полный вес автомобиля давит на поверхность площадью 2-3 см^2.