
Я делаю проект, связанный с траекториями полета. Если нам даны две точки в пространстве(lat,long) и полетные заголовки (углы), которые полет должен достичь в этих точках.
Используя формулу радиуса поворота, я проверил, может ли полет достичь следующей точки или нет, но как я могу проверить, может ли полет достичь обеих точек с указанным курсом или нет??
Пожалуйста, помогите мне.. Спасибо заранее…
Извините за двусмысленность в вопросе. На рисунке прилагается, если мне нужно пройти через точки 1, 2 и 3, поэтому на которых несколько точек на пути полета. И если мне дают (лат,Лонг,направление полета должно достичь в этой точке) для каждой точки, мне нужно выяснить, можно ли достичь точек или нет. Также, пожалуйста, предложите мне решение, если мне нужен тот же заголовок во всех трех точках (скажем, x).
И полет не должен занимать более 1 оборота, т. е. петли не допускаются (полет всегда должен двигаться к месту назначения).
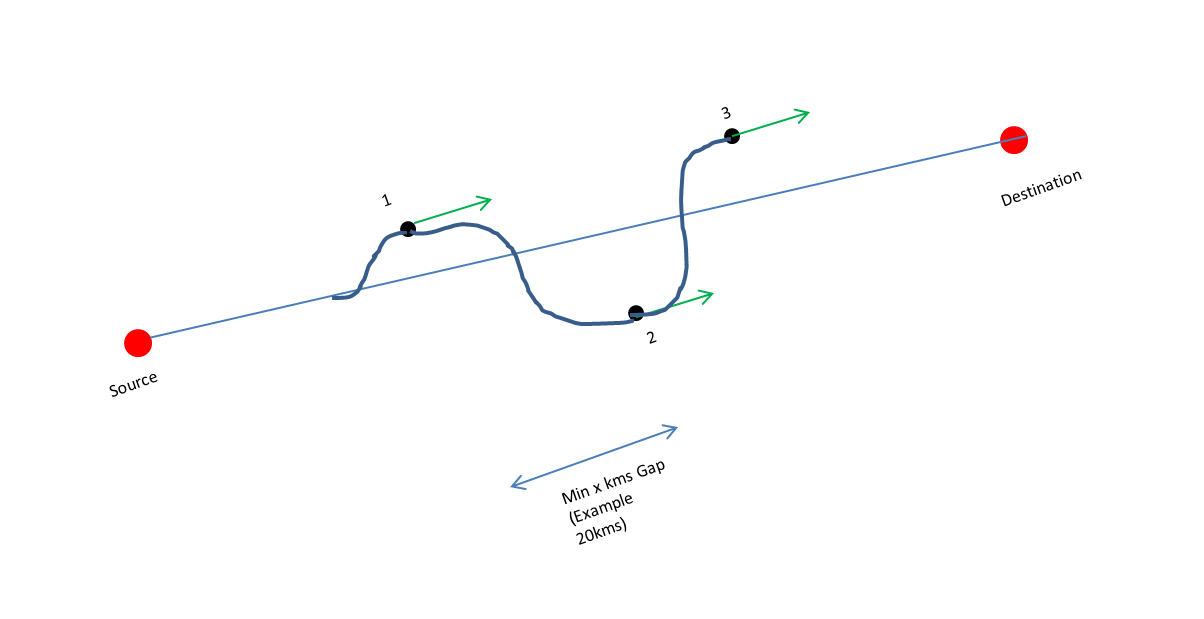
Теперь мне нужно отправиться из источника в пункт назначения по точкам 1,2,3 с тем же заголовком(q) в этих трех точках. Например, возьмите q Как угол между источником и местом назначения. Теперь я хочу двигаться к пункту назначения i.e не поворачивая назад и без петель. Просто хочу знать, возможно ли его полет с определенным радиусом поворота, чтобы достичь следующей точки или нет.
Или каково должно быть минимальное вертикальное расстояние и горизонтальное расстояние между точками, чтобы удовлетворить обе точки.
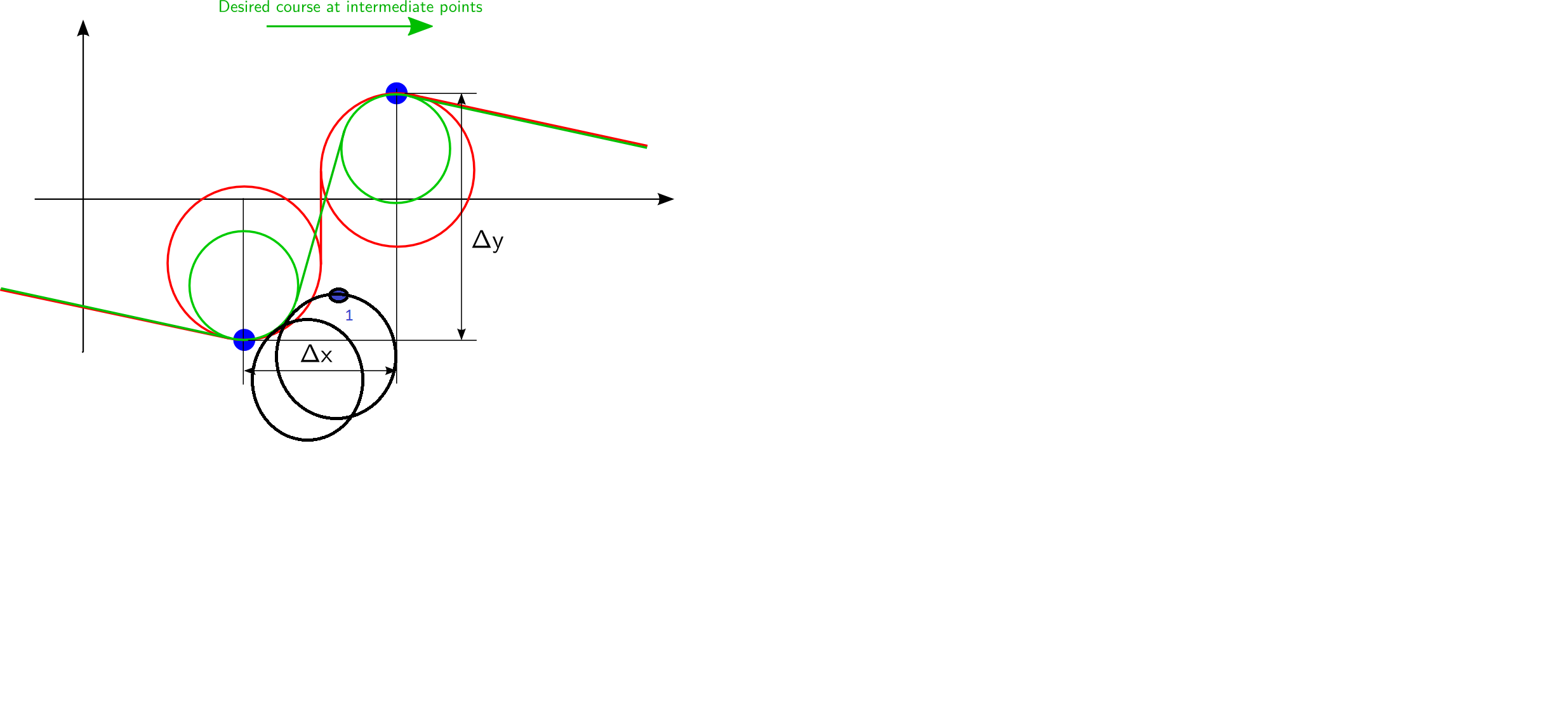
Но мы не можем точно определить минимальный радиус?? На рисунке 3, пункт 1 может быть достигнут с указанным заголовком с расстоянием ниже 2 * rmin. rmin definitely because it can’t reach close neighboring points but what should be next condition to check whether it can reach with required heading or not. » data-translation=»Таким образом, условие будет похоже на delta(x) > rmin определенно, потому что оно не может достичь близких соседних точек, но какое должно быть следующее условие, чтобы проверить, может ли оно достичь требуемого заголовка или нет. » data-type=»trSpan»>Таким образом, условие будет похоже на delta(x) > rmin определенно, потому что оно не может достичь близких соседних точек, но какое должно быть следующее условие, чтобы проверить, может ли оно достичь требуемого заголовка или нет. 2 * rmin then figure 3 would contradict it, right?» data-translation=»Если это похоже на delta (x) > 2 * rmin, то рисунок 3 будет противоречить ему, верно?» data-type=»trSpan»>Если это похоже на delta (x) > 2 * rmin, то рисунок 3 будет противоречить ему, верно?
Разница в заголовках дает вам количество градусов, которые вам нужно повернуть. Затем расстояние между двумя точками становится секущим для круга поворота, который должен дать вам радиус поворота, применяя некоторую базовую геометрию. Я предполагаю, что поворот начинается с точки 1 и заканчивается на достижении точки 2. Вроде этого:
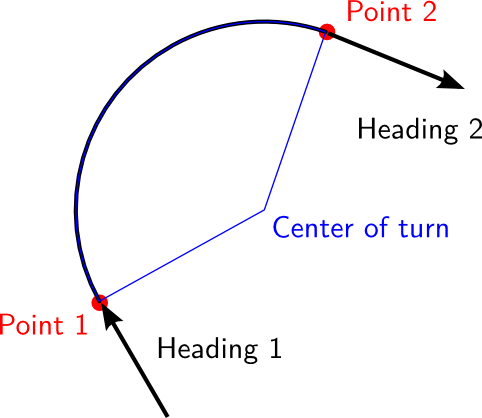
Теперь вам сначала нужно вычислить радиус поворота, используя уравнение для секущей длины: начните с разности между двумя заголовками и назовите этот угол φ
. Тогда разница между двумя точками с
есть
Поскольку вы знаете с
, вы можете рассчитать радиус поворота р
простым преобразованием:
Теперь нужно проверить, сможет ли самолет развернуться с таким радиусом. Это зависит от нагрузки на крыло mS
, плотность воздуха ρ
и максимальный коэффициент подъема c L m A x
, и уравнение для минимального радиуса поворота
Сравните оба значения р
и проверьте, если r» data-translation=»>» data-type=»trSpan»>>rmin
. Тогда поворот физически возможен.
Теперь я только надеюсь, что это действительно то, что вы просили. Ваш вопрос оставляет много места для интерпретации.
Изменить: @amarender обновил вопрос. Теперь заголовок идентичен во всех промежуточных точках, а ниже-одно из многих возможных решений (синяя линия):
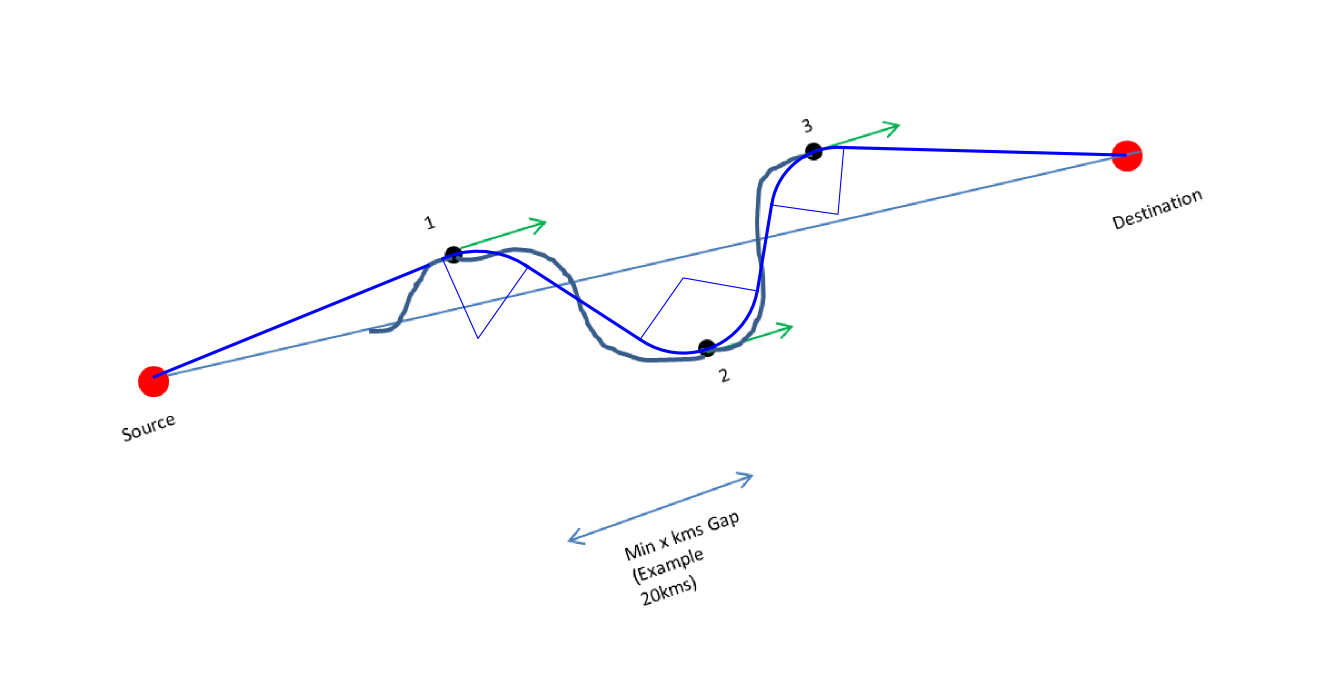
Я указал с сегментами пирога, где повороты; конечно, одно единственное условие поворота должно интерпретироваться как один поворот на промежуточную точку. Участки между поворотами прямые, и все они приближают воздушное судно к месту назначения, если курс в промежуточных точках идентичен курсу от цели к месту назначения.
Когда у нас есть условие, при котором решение невозможно? Только если точки находятся слишком близко друг к другу для выполнения условия минимального радиуса поворота. Поворачивая систему координат таким образом, чтобы желаемый курс в точках был параллелен оси x, это легче показать:
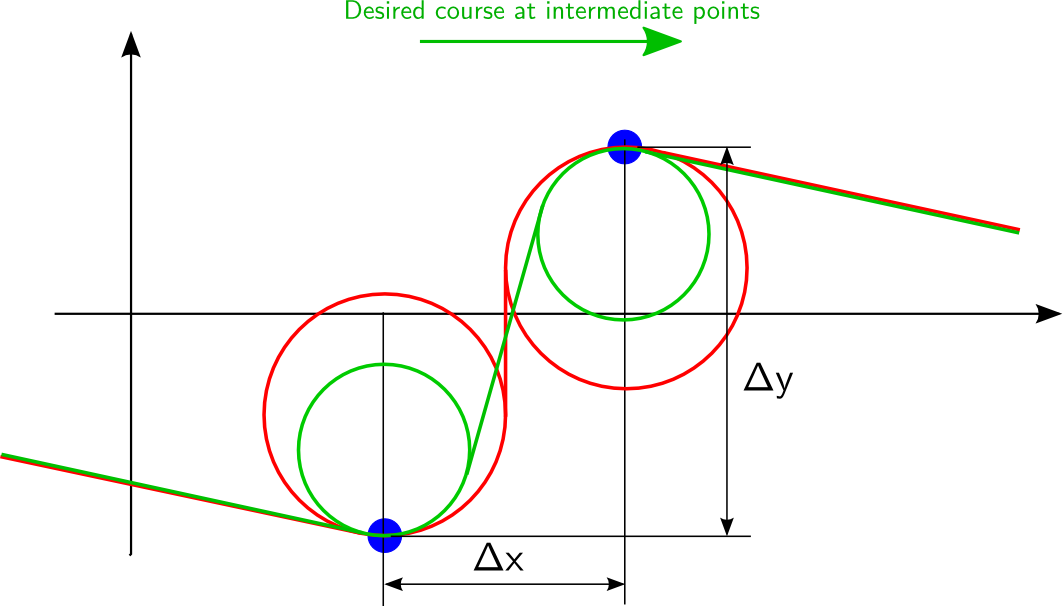
Расстояние между двумя точками в направлении нужного курса Δx
не должно быть меньше диаметра минимально возможного круга (2⋅rmin
) используя уравнение выше . Зеленая линия выше для Δx» data-translation=»>» data-type=»trSpan»>>2⋅rmin
, и красная линия для граничного условия Δx=2⋅rmin
. Чтобы быть точным, приведенное выше уравнение не ограничивает максимальный коэффициент нагрузки n z m A x
— если это необходимо учитывать, минимальный радиус:
Все становится сложнее, когда заголовок в точках отличается от заголовка из источника в пункт назначения. Затем Δy
становится важным, а также, и когда он становится большим относительно Δx
, прямая связь между поворотами будет указывать от цели очень скоро.
это на самом деле только одна из 12 возможных ситуаций (при условии одинаковой высоты для обеих точек). Как я уже сказал в своем комментарии к вопросу, это всегда возможноreach both the points with the specified heading, этот ответ проверяет, только если это возможно, выполняя только один ход.
@Федерико: вы правы, я догадался, что amarender может означать. Но полет по произвольному пути между двумя точками тривиален,поэтому я взял случай с самой короткой круговой связью между ними.
Я понимаю, что я взял на себя смелость подчеркнуть это, так как вы явно не изложили предположение в своем ответе. Кроме того, существуют оптимальные решения, когда r<rmin
, но они включают несколько поворотов.
Я бы поспорил, что OP просит достичь обеих точек за один ход, где поворот меньше 180 градусов, а плоскость все время вращается с постоянной скоростью между двумя точками. В противном случае поворот всегда возможен путем промаха, а затем поворота в противоположном направлении. Если более одного поворота позволяет, то вопрос спорный, есть бесконечное количество решений.
Что делать, если мне нужен одинаковый угол направления во всех точках, и полет не может занять более одного поворота.e если он все время направляется только к месту назначения.Полет также не может принимать петли. Представьте себе только один источник и один пункт назначения и точки 1,2,3 лежат между ними.

Если вы можете проверить один, вы можете проверить следующий после этого таким же образом, нет?
Теги довольно выключены, а заголовок также не описателен. Кроме того, вы всегда можете добраться до другого места, только вопрос в том, сколько маневров вам нужно сделать, чтобы получить указанный результат.
Это больше похоже на геометрическую головоломку, чем на авиационный вопрос. Если мы не знаем начальных и конечных точек, как нам помочь с оптимальным маршрутом, учитывая, что вам нужно избегать поворотов? Я чувствую себя экспертом в этом видео .
@amarender: пожалуйста, укажите вашу проблему со всеми граничными условиями. Я ожидаю, что вы поможете себе больше всего, когда четко выразите то, что именно вы хотите знать.
@amarender: обратите внимание, что на втором рисунке у вас есть 2 оборота между каждой парой точек.