flyman Админ. спросил 4 года назад
Меня смущает эта идея. Если поток устойчив, его линии потока неизменны. Беря типичный пример аэродинамического профиля, есть (по крайней мере) один поток, который ударит по передней кромке аэродинамического профиля и застынет. Точка застоя определяется как:
точка в поле потока, где локальная скорость жидкости равна нулю.
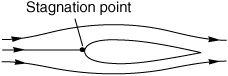
Теперь мой вопрос: если скорость здесь равна нулю, а частицы жидкости, которые проходят через поток, который приводит к точке застоя, имеют ненулевую скорость вверх по течению, куда идут эти частицы жидкости? Поскольку они находятся на обтекаемой линии, они должны достичь точки застоя? Разве это не противоречит закону сохранения массы?
Кроме того, онлайн-курс механики жидкости, который я следовал, в одной лекции показал линии тока, уходящие от точки застоя . Если скорость в этой точке точно равна нулю (и неизменна, поскольку поток устойчив), то как частицы жидкости могут идти в других направлениях?
Должно быть, я что-то упускаю, просвети меня.
flyman Админ. ответил 4 года назад
Идея точки застоя-это идеализация. Эта точка бесконечно мала, и частицы воздуха, протекающие вдоль потока, который ведет в нее, будут замедляться на своем пути. Чем ближе они подходят к точке застоя, тем медленнее они текут, и в конце концов они никогда не достигают точки застоя.
В действительности, молекулы воздуха имеют конечный размер, поэтому они текут либо выше, либо ниже точки застоя потока. Даже если одной частице удастся достичь точки застоя и остаться на месте (что теоретически невозможно), небольшой угол изменения атаки смоет ее в следующий момент.
Один поток уходит от задней точки застоя, которая расположена в задней кромке. Эта точка идеализирована вдвойне, потому что она требует, чтобы невязкий поток имел заднюю точку застоя. Опять же, молекулы, протекающие вдоль стенки аэродинамического профиля, будут замедляться давлением точки застоя, чем ближе они к задней кромке. Поскольку они прибывают либо выше, либо ниже задней точки застоя, они ускоряются, как только они прошли точку наивысшего давления, и движутся выше или ниже потока, исходящего из задней точки застоя.
Однако концепция точки застоя действительно полезна для понимания явлений потока. Существует действительно линия (в 3D это плоскость), которая отделяет воздух, который будет течь по крылу от того, что будет течь под ним. Эта линия изменяет с углом нападения, и простая лопасть предупреждения стойла основана на этом принципе. Как только линия заканчивается ниже лопасти, воздух будет нажимать на нее вверх, закрывая электрический контакт, который активирует зуммер в кабине.
Флюгер предупреждения стойла (маленькая металлическая штуковина, торчащая из крыла)
flymanКогда вы говорите заднюю точку застоя, вы имеете в виду точки застоя на задней кромке аэродинамического профиля?
Кроме того, чтобы подтвердить то, что я просил. Тогда теоретически невозможно для устойчивого потока иметь точку застоя, верно?
@midnightBlue: да, задняя точка застоя находится на задней кромке. В идеале. Если ваше понимание точек застоя заключается в том, что они собирают молекулы воздуха, которые никогда не покинут их, то да, их не существует в практической жизни. Они практически невозможны, но теоретически они очень живы (но бесконечно малы).
Отлично! Думаю, теперь я начинаю понимать это немного лучше. Знаете ли вы, что такое чувствительность сигнальной лопасти? (внезапное временное изменение угла атаки может вызвать предупреждение о сбое?). Кроме того, является ли расположение и угол установки предупреждающей лопасти приблизительно лучшим выбором? (т. е. при определенных различных условиях, будет ли предупреждающая лопасть лучше располагаться в другом месте с другим заданным углом?)
@midnightBlue: расположение и частота является результатом тестирования. Вы хотите некоторую маржу, но вещь не должна постоянно уходить. Чувствительность неплохая: порыв ветра в медленном полете может спровоцировать его, но тогда вы можете быть уверены, что крыло в этом месте находится всего в нескольких градусах от остановки, поэтому вам лучше ускорить. При хорошей посадке предупреждение прозвучит за несколько секунд до того, как колеса коснутся земли.
flyman Админ. ответил 4 года назад
Точка застоя в потоке не бросает вызов закону сохранения массы. Петер Кэмпф уже объяснял, что это идеализация, которая помогает понять явления потока.
Тот факт, что скорость равна нулю в точке вдоль линии потока, не означает, что масса собирается в этой точке. Вы можете сравнить его со знаком остановки на дороге. Машины подъезжают к знаку, останавливаются и снова останавливаются. Пока есть достаточное пространство между последовательными автомобилями, это может быть непрерывным процессом, представляющим устойчивый поток.
Принимая эту аналогию далее, точка застоя на переднем крае 2D-профиля похожа на Т-образный переход на дороге с односторонним движением. Автомобили, прибывающие на Т-образный перекресток, останавливаются и продолжают либо левый, либо правый поворот и следуют по их путям. Молекулы воздуха достигают точки застоя и продолжаются оттуда либо по верхней, либо по нижней части профиля.
flyman Админ. ответил 4 года назад
Скорость-явление мгновенное. Она существует в какой-то момент.(давайте проигнорируем среднюю скорость здесь, нет необходимости обсуждать ее для этого вопроса.) В точке застоя скорость равна 0. Однако на расстоянии dx от точки застоя частица жидкости снова набирает обороты. Это похоже на маятник. В самой высокой точке его скорость равна нулю, но через дифференциальное время dt он снова восстанавливает свою скорость и начинает двигаться. Вы видите, что частицы жидкости, такие как маятник, нуждаются в стимуле, чтобы сделать это, в случае маятника его гравитация, для частицы жидкости это может быть что угодно: от силы давления до инерции
Общее недоразумение заключается в том, что частицы воздуха не неподвижны , когда мы говорим, что есть ветер с нулевой скоростью (или воздушный поток), иначе давление упадет до нуля. Точка застоя-это бесконечно малый объем, в котором скорость воздушного потока равна нулю. Это математическая модель определения, а не физическая реальность
«жидкие частицы, которые проходят через поток» в стационарном потоке, являются траекториями, и участки не могут пересекать их. Участок между двумя линиями в этом случае всегда будет находиться между этими двумя линиями.
Никакая масса не пересекает линии потока. Таким образом, частицы жидкости находятся непосредственно выше и ниже потока, заканчивающегося в точке застоя.