Как рассчитать угловую скорость и радиус поворота?

Вопросы / ответы › Как рассчитать угловую скорость и радиус поворота?

0 +1 -1

flyman Админ. спросил 5 лет назад

Как я могу вычислить с известными касательными разных углов и по эмпирическим правилам?

Какие формулы следует использовать для fps и NM?

Источник

Теги вопроса:аэродинамика, аэродинамики

flyman Админ. ответил 5 лет назад

Что вы подразумеваете под «касательными углов»?

flyman Админ. ответил 5 лет назад

математические постоянные значения

4 ответ

0 +1 -1

flyman Админ. ответил 5 лет назад

Ваша терминология немного запутана, но я собираюсь предположить, что вы спрашиваете, как рассчитать радиус поворота и скорость поворота на основе скорости и угла крена. Эти формулы можно найти в руководстве пилота FAA по Аэронавтическим знаниям, которое доступно бесплатно онлайн.

В справочнике приведены формулы скорости поворота и радиуса поворота на стр. 4-34:

R = \frac{V^{2}}{11.26 \tan θ}

$R=\frac{V^2}{11.26\tan\theta}$

ω = \frac{1, 091 \tan θ}{V}

$\omega=\frac{1,091\tan\theta}{V}$

Используемые переменные:

$V$
$R$
$θ$
$ω$

Например, на 120 узлах и угле крена 30°, радиус поворота и тариф поворота:

R = \frac{120^{2}}{11.26 \tan 30} = \frac{14, 400}{11.26 \times 0.5773} = 2, 215 f e e t \approx \frac{1}{3} n a u t i c a l m i l e

$R=\frac{120^2}{11.26\tan30}=\frac{14,400}{11.26\times0.5773}=2,215 feet\approx\frac13nautical~mile$

ω = \frac{1, 091 \tan 30}{120} = \frac{1, 091 \times 0.5773 \tan 30}{120} = 5.25 ° / s e c

$\omega=\frac{1,091\tan30}{120}=\frac{1,091\times0.5773\tan30}{120}=5.25°/sec$

«Магические константы» в этих формулах ( $11.26$

11.26

$11.26$ и $1, 091$

1, 091

$1,091$ ) коэффициенты пересчета для задействованных единиц (узлы, ноги и степени). Физики использовали бы единичные формулы, включающие $g$

g

$g$ , ускорение из-за силы тяжести (примерно $9.8 m / s e c^{2}$

9.8 m / s e c^{2}

$9.8m/sec^2$ ).

Вы также можете переставить формулы выше, используя простую алгебру, чтобы выяснить требуемый угол банка, учитывая желаемую скорость поворота или радиус поворота.

Наконец, обратите внимание, что все становится намного сложнее, если вы учитываете ветры наверху . Скорость поворота всегда будет одинаковой независимо от ветра, но радиус поворота больше не применяется, потому что самолет будет отслеживать спиральный путь вдоль земли, а не круг. Поворот будет » острее «на подветренной части поворота и» шире » на подветренной части. Вот почему получается точка это сложный маневр, изучаемый в базовой летной подготовке: для того, чтобы летать по круговой наземной трассе, пилот должен постоянно изменять угол крена самолета в зависимости от ветра: нижний угол крена вверх по ветру, более высокий угол крена вниз по ветру. Пилот также должен правильно использовать руль, чтобы постоянно поддерживать координацию поворота.

Другие полезные ссылки:

Руководство пилота по аэронавигационным знаниям (цитируется выше)
Авиационный формуляр имеет раздел по поворотам
Стандартная скорость поворота статьи в Википедии
Статья Banked turn в Википедии

Есть также некоторые «связанные вопросы» в правой части этой страницы, которые могут быть полезны.

flyman Админ. ответил 5 лет назад

Физик никогда не использовал бы единую формулу. Они очень осторожны со своими подразделениями. Однако они будут использовать последовательную единичную систему (из которых SI является наиболее широко используемой, но существуют и последовательные единичные системы, основанные на обычных единицах США).

flyman Админ. ответил 5 лет назад

@JanHudec я думаю, вы неправильно поняли, что я имел в виду под «unitless»-я имел в виду, что формула не будет содержать единиц преобразования терминов и будет unit-agnostic (вы можете смешивать и сопоставлять единицы все, что вы хотите, пока вы делаете правильный размерный анализ, чтобы выяснить, какие единицы выходят в результате входов).

flyman Админ. ответил 5 лет назад

dvnrrs, спасибо за ваш ответ. Вы не используете эти два эмпирических правила, не так ли?

flyman Админ. ответил 5 лет назад

@user1876 я не делаю ничего из этого в кабине. Я использую координатор поворота, и я также летал достаточно часов, что я просто знаю, что угол крена должен быть на скоростях полета, которые я летаю. Если у вас нет простого способа увидеть стандартную ставку в кабине, на мой взгляд, этот расчет должен быть чем-то, что вы делаете на земле, и просто запомните значения. Сохраните свои мозги в кабине для чего-то другого, например, для хорошего сканирования инструмента.

flyman Админ. ответил 5 лет назад

Я не могу напрямую редактировать ответ, но в первой формуле он должен быть V^2, а не V_2.

0 +1 -1

flyman Админ. ответил 5 лет назад

После всех этих ответов с имперскими единицами позвольте мне объяснить это с единицами Си, начиная с первых принципов. R-радиус, v-скорость полета, m-масса,g — гравитационная постоянная, Φ — угол крена и L-подъем.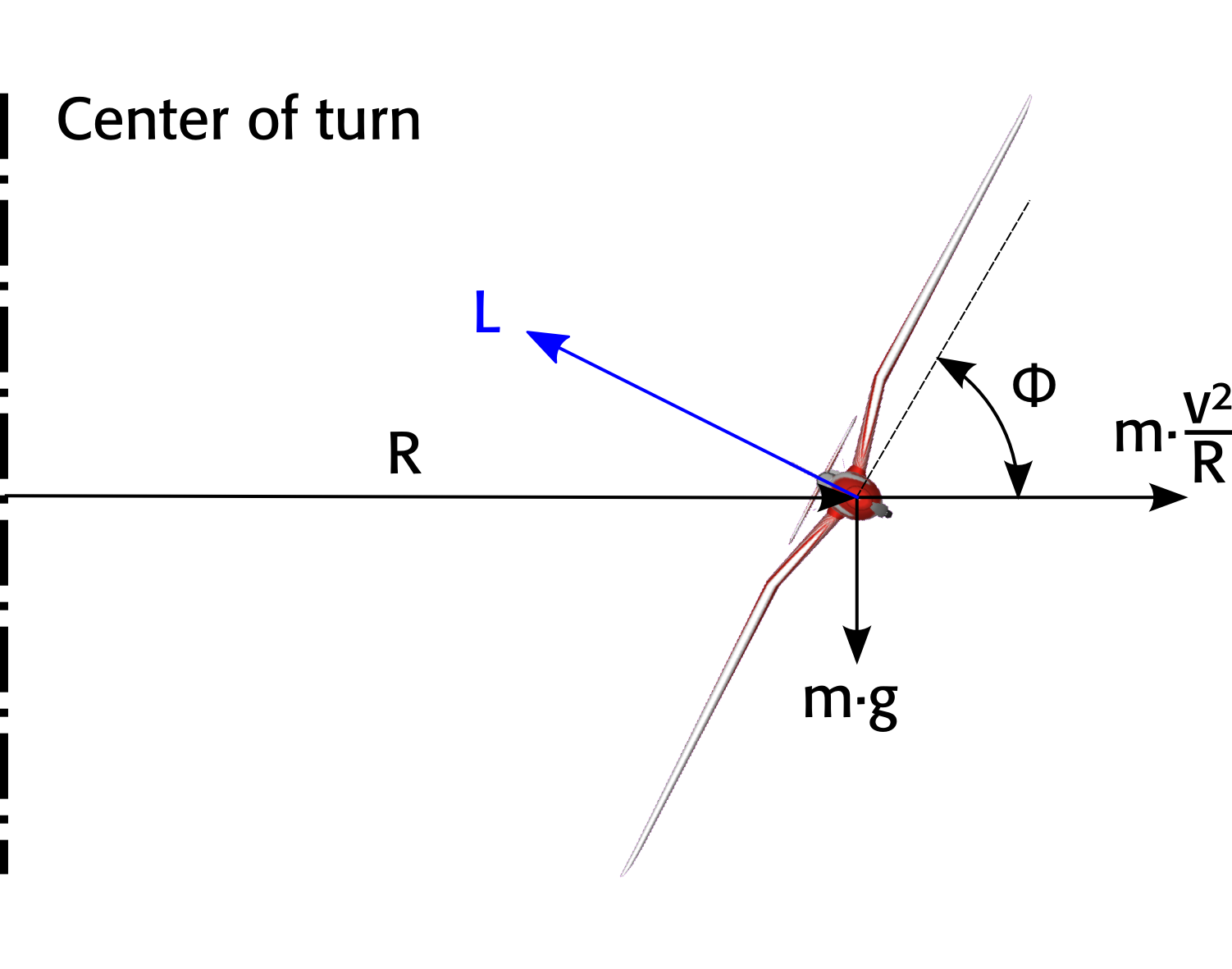 Самолет в банковском полете

Подъем должен быть равен весу (m·g) и центробежной силе (m·ω2·R = m· $\frac{v^{2}}{R}$

\frac{v^{2}}{R}

$\frac{v^2}{R}$ ), так

L = \sqrt{(m \cdot g)^{2} + (m \cdot ω^{2} \cdot R)} = \frac{ρ}{2} \cdot v^{2} \cdot c_{L} \cdot S

$L = \sqrt{(m{\cdot}g)^2 + (m{\cdot}{\omega}^2{\cdot}R)} = \frac{\rho}2{\cdot}v^2{\cdot}c_L{\cdot}S$

с ρ плотность воздуха, $c_{L}$

c_{L}

$c_L$ коэффициент подъемной силы и S площадь поверхности крыла. Теперь конвертируйте, чтобы вы получили v:

v = \sqrt[4]{\frac{(m \cdot g)^{2}}{(\frac{ρ}{2} \cdot c_{L} \cdot S)^{2} - (\frac{m}{R})^{2}}}

$v = \sqrt[\Large{4\;}]{\frac{(m{\cdot}g)^2}{{(\frac{\rho}2{\cdot}c_L{\cdot}S)^2} - (\frac{m}{R})^2}}$

Теперь вы можете видеть, что номинатор не может стать нулевым или меньше, что дает вам минимальный радиус для заданной скорости и максимального коэффициента подъема $c_{L m a x}$

c_{L m a x}

$c_{L max}$ :

R \geq \frac{2 \cdot m}{\frac{ρ}{2} \cdot c_{L m a x} \cdot S},

$R ≥ \frac{2{\cdot}m}{\frac{\rho}2{\cdot}c_{L max}{\cdot}S},$ и вообще:

R = \frac{2 \cdot m}{\frac{ρ}{2} \cdot c_{L} \cdot S} = \frac{v}{ω} = \frac{v^{2}}{g \cdot \sqrt{n_{z}^{2} - 1}}

$R = \frac{2{\cdot}m}{\frac{\rho}2{\cdot}c_{L}{\cdot}S} = \frac{v}{\omega} = \frac{v^2}{g\cdot\sqrt{n_z^2-1}}$

Это похоже на «радиусный барьер»: повороты не могут лететь плотнее, чем это. Это происходит из-за увеличения центробежной силы, которая прибывает из более крутых поворотов полета. Чем круче поворот, тем быстрее вы должны лететь, чтобы создать достаточный подъем для компенсации веса и центробежной силы.

Что все еще увеличивается, так это ваша угловая скорость ω:

ω = \frac{v}{R} = \frac{g \cdot t a n Φ}{v} = \frac{g \cdot \sqrt{n_{z}^{2} - 1}}{v}

${\omega} = \frac{v}{R} = \frac{g{\cdot}tan{\Phi}}{v} = \frac{g\cdot\sqrt{n_z^2-1}}{v}$

Внизу я построил планер. Вы можете ясно видеть радиус барьера на 40 м. Поверьте мне, это выглядит точно так же для авиалайнера, только цифры больше.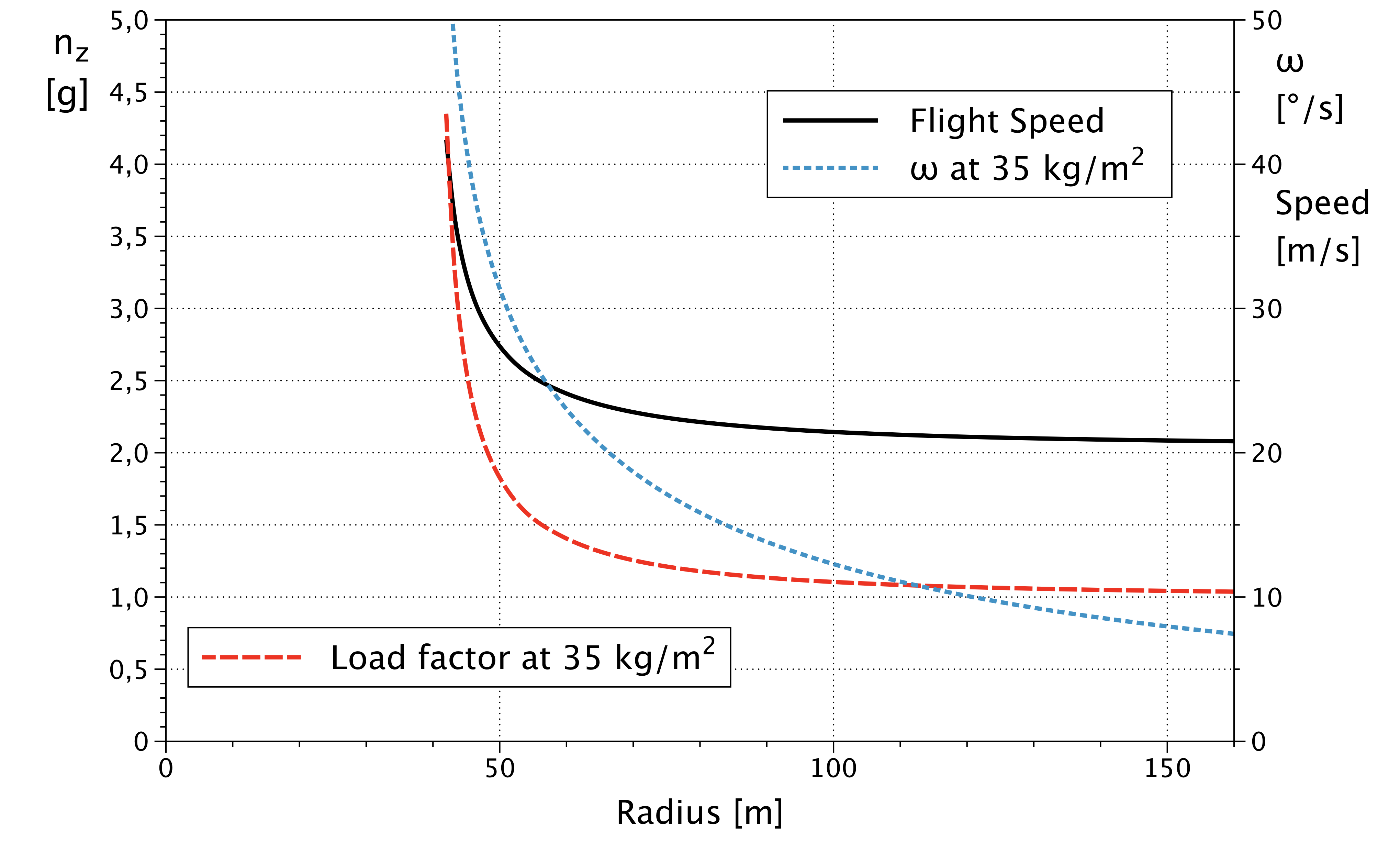 участок для скорости, nz и омега по радиусу

Если вам нужна быстрая формула для оценки радиуса, вам нужно использовать квадрат воздушной скорости, так что это не простая линейная зависимость. Для поворота с креном 30° ( $n_{z}$

n_{z}

$n_z$ = 1.15), знаменатель уравнения радиуса составляет около 4, поэтому, чтобы вычислить радиус поворота в метрах, разделите квадрат воздушной скорости на 4 или возьмите квадрат половины вашей воздушной скорости в метрах в секунду.

Для скорости поворота в градусах в секунду разделите 220 на скорость полета в метрах в секунду. Полет медленнее позволяет более высокую скорость поворота.

Теперь о другой крайности: гиперзвуковым самолетам нужно много места для маневрирования. У меня есть здесь некоторые ценности, просто для удовольствия: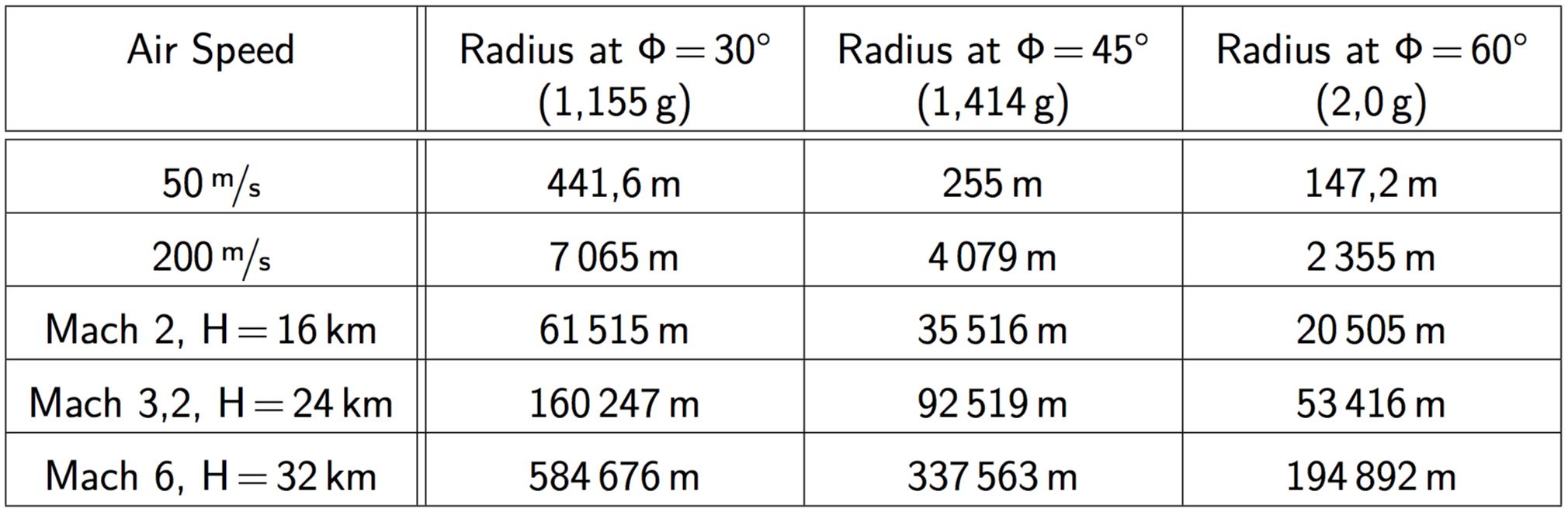 таблица радиусов превышения скорости

Высокая скорость делает это почти терпимым, в конце концов, половина оборота на Mach 6 и 2 g занимает всего 336 секунд, то есть менее 6 минут. Авиалайнеры крен только 30° или меньше, поэтому первая колонка действительна, если вы летите ваш гиперзвуковой автомобиль, как авиалайнер.

flyman Админ. ответил 5 лет назад

Наконец, правильный ответ SI с небольшим фоном для него! Там нет необходимости, чтобы получить коэффициент подъема участие, хотя, не делают его слишком сложным. Но если вы хотите сделать комплекс, то учтите, что на высоких скоростях ваш кажущийся вес меньше. Радиусы поворота, которые вы рассчитали, слишком низки для Mach 6 (фактически вес примерно на 10% меньше, поэтому радиус примерно на 10% больше, если двигаться на восток на Mach 6 выше экватора)

flyman Админ. ответил 5 лет назад

@DeltaLima: вы правы, но я не хотел, чтобы сделать его слишком сложным 😉

flyman Админ. ответил 5 лет назад

@Питер, не было бы проще (или, по крайней мере, эквивалентно) просто использовать Пифагор, и обратите внимание, что в любом повороте самолет всего G (T) является гипотенузой, радиальный G (R) является горизонтальной составляющей, а один (1) G является вертикальной составляющей, поэтому вы можете использовать формулу $R^{2} » role=»presentation»>$

$R^2$ + 1 = $T^{2} » role=»presentation»>$

$T^2$ и радиус поворота = $V^{2} » role=»presentation»>$

$V^2$ / Радиальный G = $V^{2} » role=»presentation»>$

$V^2$ / ( $T^{2} » role=»presentation»>$

$T^2$ — 1)?

flyman Админ. ответил 5 лет назад

@CharlesBretana: самая первая формула в ответе уже применяется Пифагор. Я выразил R в терминах $c_{L} » role=»presentation»>$

$c_L$ , но, конечно, я могу добавить больше способов вычислить его.

flyman Админ. ответил 5 лет назад

@Питер, да, я видел это. Это не означало, что ваш ответ опустил или проигнорировал этот факт, просто что это может быть более простой вывод, чтобы начать с формулы Пифагора, выраженной в G — единицах, а не поднимать силы. Я предполагал, что, сделав это, вы можете получить результат с меньшим количеством шагов. Нет biggy, хотя.

0 +1 -1

flyman Админ. ответил 5 лет назад

Если вы собираетесь делать это в кокпите, хорошее эмпирическое правило поможет больше, чем точная формула:

Угол крена для тарифа 1 оборот $\frac{s p e e d}{10} + 7$
$\frac{s p e e d}{10} + 7$
$\frac{speed}{10}+7$ .

Диаметр поворота составляет 1% от скорости.

например. для поворота 120кц вам $\frac{120}{10} + 7 = 19 °$

\frac{120}{10} + 7 = 19 °

$\frac{120}{10}+7=19°$ банка и имеют $\frac{120}{100} = 1.2$

\frac{120}{100} = 1.2

$\frac{120}{100}=1.2$ диаметр поворота Нм

flyman Админ. ответил 5 лет назад

Из любопытства вам когда-нибудь приходилось делать это в кабине пилотов? Я всегда удивлялся и никогда не думал о себе.

flyman Админ. ответил 5 лет назад

Угол банка может быть, пару раз в G1000, где ставка 1 «трудно увидеть», поскольку нет надлежащего координатора поворота, поэтому я бы предпочел нацелиться на конкретный банк и удерживать его. Диаметр витка не так много…

0 +1 -1

flyman Админ. ответил 5 лет назад

Другой подход заключается в том, чтобы просто отметить, что в любом повороте уровня связь между общим самолетом G ( $G_{T}$

G_{T}

$G_T$ ), радиальный G ( $G_{R}$

G_{R}

$G_R$ ), и Божья G должна соответствовать Пифагору.

так
$G_{T}^{2} = G_{R}^{2} + 1$

G_{T}^{2} = G_{R}^{2} + 1

$G_T^2 = G_R^2 + 1$
или,
$G_{R} = \sqrt{G_{T}^{2} - 1}$

G_{R} = \sqrt{G_{T}^{2} - 1}

$G_R = \sqrt{G_T^2 - 1}$

а так как радиус поворота равен квадрату скорости над радиальным G,

R = \frac{V^{2}}{\sqrt{G_{T}^{2} - 1}}

$R = \frac{V^2}{\sqrt{G_T^2 - 1}}$

общий самолет G, конечно, это просто лифт, разделенный на вес самолета.и если мы находимся ниже скорости маневрирования (самая низкая скорость полета, при которой мы можем генерировать коэффициент нагрузки G-Limit) и поворачиваемся на максимальный угол атаки (AOA), то подъем самолета $C_{L m a x} p V^{2} S$

C_{L m a x} p V^{2} S

$C_{Lmax} p V^2 S$ и вес, конечно, может быть представлен подъемом произведенным на АТ $C_{L} m a x$

C_{L} m a x

$C_Lmax$ когда на скорости стойла или $C_{L m a x} p V_{s}^{2} S$

C_{L m a x} p V_{s}^{2} S

$C_{Lmax} p V_s^2 S$ .

Так что всего самолетов G, ( $G_{T}$

G_{T}

$G_T$ ), который просто поднимает разделенный весом, можно представить как $\frac{C_{L m a x} p V^{2} S}{C_{L m a x} p V_{s}^{2} S}$

\frac{C_{L m a x} p V^{2} S}{C_{L m a x} p V_{s}^{2} S}

$\frac{C_{Lmax} p V^2 S}{C_{Lmax} p V_s^2 S}$ или $\frac{V^{2}}{V_{S}^{2}}$

\frac{V^{2}}{V_{S}^{2}}

$\frac{V^2}{V_S^2}$

Подставляя в Формулу радиуса поворота, мы получаем формулу радиуса поворота для поворота максимальной производительности уровня (ниже скорости маневрирования), выраженную как функция истинной воздушной скорости самолета и скорости сваливания самолета (в True):

R = \frac{V^{2} V_{s}^{2}}{g (\sqrt{V^{4} - V_{s}^{4}})}

$R = \frac{V^2 V_s^2}{g (\sqrt{V^4-V_s^4})}$

где:

$R$
$V$
$V_{S}$
$g$

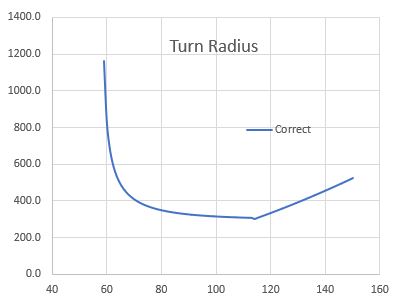
График, он выглядит так, как показано ниже: это для самолета со скоростью сваливания 58 kt (правда) и плакатом G-limit 3,8 Gs. (Излом при 122 КТ происходит из-за того, что, как только мы быстрее маневрируем, мы ограничены плакатом G и больше не можем достичь $C_{L m a x}$

C_{L m a x}

$C_{Lmax}$ без разрушения или перенапряжения планера.)