Как начать вывод продольных уравнений движения самолета?

Примечание: ответ в процессе!

Часть 1 (к сожалению, я знаком только с #1 и #3 на данный момент, а не #2)

(Сноска: это может быть немного проще, чем ваш случай, но, надеюсь, вы сможете заполнить оставшиеся пробелы)

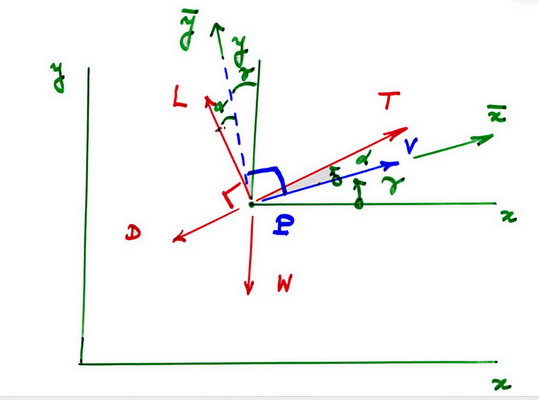
Из этого вы можете использовать некоторые силы в соответствии с направлением скорости или вектором подъема. Делая это горизонтально, вы получаете уравнение 1, а также для вертикального направления вашего уравнения 3.

Чтобы сделать это проще в обращении, мы используем малоугловое приближение рассмотрим cos (0 ) = 1

$\cos(0)=1$ и sin (0 ) = 0

$\sin(0)=0$. Это упрощает вниз:

$$V:0=T-D$$

$$L:0=mg-L$$

(т. е. тяга равна сопротивлению, подъем равен весу)

Часть 2:

Это в основном уравнения кинетической диаграммы диаграммы диаграммы свободного тела выше, где может быть изменение либо в воздушной скорости высоты. То, что говорит ваше второе уравнение, заключается в том, что избыточная тяга (T-D, Thrust-Drag) может:

• используйте для увеличения высоты: m×g×sin(y)
  $m\times g\times \sin (y)$

  $m\times{g}\times\sin(y)$

и-или

• используйте для увеличения воздушной скорости: M × v
  $m\times v$

  $m\times{v}$

Зависит от того, что вы подразумеваете под «вывести уравнения». Если вы действительно имеете в виду, что хотите работать над этой формулировкой, начиная с основ, ну, вы начинаете с старого доброго Ньютона:

$$\overrightarrow{F}=m\overrightarrow{A}$$

и эквивалент для моментов (→

$\overrightarrow{}$ указывает векторы).

На этом этапе вам нужна система отсчета, в которой можно разложить ваши векторные уравнения (неподвижные тела, неподвижные земли, оси устойчивости: выбор влияет на то, какие термины вы сможете упростить позже) и описание вашей системы: какие силы применяются на самолете? как я могу описать их как функции состояния самолета?

В этот момент Вы подставляете в исходное уравнение и продолжаете вычисление.

Вы можете ознакомиться с этими слайдами лекции, чтобы увидеть шаг за шагом, как это можно сделать. Лекция 8 и 9 для общего случая 6DoF и лекция 11 для вашего конкретного вопроса.